[IJNME21] Lagrangian‐Eulerian Multi‐Density Topology Optimization with the Material Point Method
Abstract
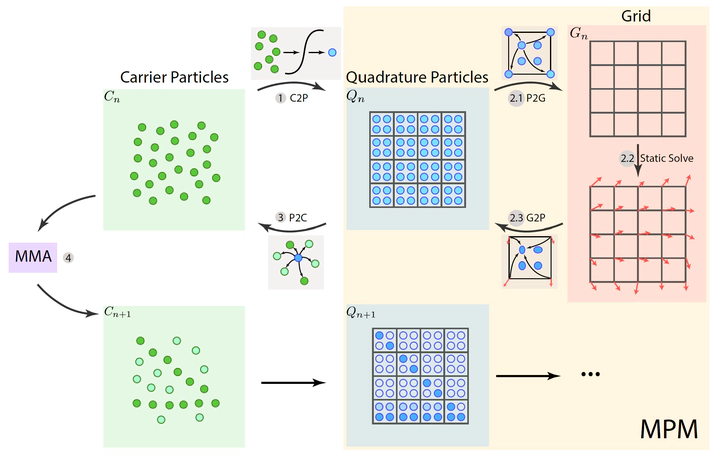
In this paper, a hybrid Lagrangian‐Eulerian topology optimization (LETO) method is proposed to solve the elastic force equilibrium with the Material Point Method (MPM). LETO transfers density information from freely movable Lagrangian carrier particles to a fixed set of Eulerian quadrature points. The transfer is based on a smooth radial kernel involved in the compliance objective to avoid the artificial checkerboard pattern. The quadrature points act as MPM particles embedded in a lower‐resolution grid and enable a sub‐cell multi‐density resolution of intricate structures with a reduced computational cost. A quadrature‐level connectivity graph‐based method is adopted to avoid the artificial checkerboard issues commonly existing in multi‐resolution topology optimization methods. Numerical experiments are provided to demonstrate the efficacy of the proposed approach.
Minchen Li
Assistant Professor
